Решение олимпиадных заданий по математике 11 класс

Решение заданий олимпиады по математике 11 класс

Задание 1.

Разложим число 2007 на простые множители: 2007 = 3² х 223.
В разложении на простые множители числа 2007! показатель степени у числа 3 будет достаточно большим, так как множитель 3 входит в разложение каждого третьего числа.
Множитель 223 входит только в разложение чисел вида 223р,
где р – натуральное число, не превосходящее 9.
Таким образом, в разложение числа 2007! на простые множители число 223 войдет с показателем 9.
Следовательно, число 2008! будет делиться на 2007^k, где k = 9.

Задание 2.

Координаты вершины параболы
x₀ = (a + 1)/2, y₀ = 4((a + 1)/2)² - 4(a +1)(a + 1)/2 + a = -a² - a - 1 = -(a + 1/2)² - 3/4.
Так как у₀ < 0 при любых значениях а, то во второй координатной четверти вершина параболы находиться не может.

Задание 3.

Так как разность прогрессия положительна, то прогрессия – возрастающая.
Следовательно, описанная ситуация возможна тогда и только тогда,
когда члены прогрессия с первого по 2008-ой – отрицательны, а начиная с 2009-го – положительны.
Таким образом, S2008 будет наименьшей, тогда и только тогда, когда а₂₀₀₈ < 0, a₂₀₀₉ > 0.
Отсюда получаем систему неравенств



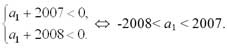
Задание 4.

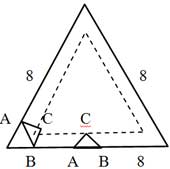
Если вершина А и В лежат на одной стороне треугольника, то вершина С лежит на отрезке прямой, параллельной этой стороне. Длина этого отрезка равна 8 - ?3. Пусть вершины А и В лежат на двух сторонах равностороннего треугольника с общей вершиной О.
Тогда вокруг четырехугольника АСВО можно описать окружность (четырехугольник является вписанным). В этой окружности углы ВАС и ВОС равны, так как опираются на одну и ту же дугу с хордой ВС.
Следовательно, угол ВОС равен 30°. Следовательно, третья вершина треугольника – точка С – лежит на биссектрисе угла равностороннего треугольника. Длина соответствующего отрезка биссектрисы равна 1.
Итак, точка С может лежать на стороне некоторого равностороннего треугольника и на некоторых отрезках биссектрис внутренних углов этого треугольника. Длина шести звеньев этой линии равна 27 - 3 x 3.



Задание 5.

если m + n – четно, то выигрывает второй игрок, если m + n – нечетно, то выигрывает первый.
В начале игры веревочек единичной длины было m(n + 1) + n(m + 1) = 2mn + m + n.
Это число имеет ту же четность, что и число m + n.
Последний ход в игре разрушает последний замкнутый контур.
Докажем, что граница любого замкнутого конура содержит четное количество веревочек единичной длины.
Действительно, рассмотрим границу произвольного замкнутого контура.
Каждый вертикальный столбец исходной сетки содержит четное количество горизонтальных веревочек единичной длины из этой границы (возможно, и нулевое), т. к. войдя в замкнутый контур, например, снизу, мы обязаны из него выйти.
Аналогично, каждая горизонтальная строка исходной сетки содержит четное количество вертикальных веревочек единичной длины.
Таким образом, общее количество единичных веревочек на границе замкнутого контура – четно.
Выигрышная стратегия для любого игрока состоит в том, чтобы не разрушать последний замкнутый контур, пока есть такая возможность.

Олимпиады по математике для 11 класса     вариант 1       вариант 2

Решения заданий олимпиады по математике для 11 класса     вариант 1        вариант 2