Парадокс Архимеда

Парадокс Архимеда. Закон Архимеда.

Закон Архимеда. Природа выталкивающей силы

Парадокс Архимеда
Парадокс Архимеда заключается в том, что любое тело может плавать в объёме воды меньшем, чем объем самого тела, если средняя плотность этого тела меньше, чем плотность воды. Таким образом, массивное тело (например, корабль) может плавать в объёме воды значительно меньшем, чем объём самого тела, при условии, что вода окружает тело со всех сторон.
Этот парадокс назван в честь известного Архимеда из Сиракуз, который открыл знаменитый закон Архимеда. Согласно этому закону сила, действующая на тело, погруженное в жидкость, равна весу вытесняего им объёма жидкости. В примере с кораблём сила Архимеда равна весу воды в объеме той части корабля, которая погружена в воду. Если вытесняющая сила больше, чем вес корабля, то он будет плавать.
Этот парадокс опирается на факт, что для силы Архимеда важен объём погружённой части плавающего тела, а не объём воды, которое это тело вытесняет.

Закон Архимеда. Природа выталкивающей силы


Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед.

Закон Архимеда

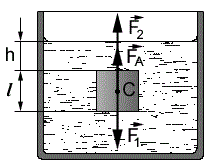
формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Рассмотрим теоретический вывод закона Архимеда. В сосуд (см. рис.) налита жидкость и погружено тело, имеющее форму куба. Ребро куба равно l. Верхняя грань куба находится от поверхности жидкости на глубине h, а нижняя - на глубине h + l. На все грани куба жидкость оказывает давление. При этом силы давления, действующие на боковые грани куба, взаимно компенсируются. На верхнюю грань куба действует направленная вниз сила давления F₁, модуль которой

F1 = r_жghS    (1)

где r_ж - плотность жидкости; S - площадь грани куба. На нижнюю грань куба действует направленная вверх сила давления F₂, модуль которой

F₂ = r_жg(h + l)S.    (2)

Так как h < h + l, то F₁<F₂, т.е. равнодействующая этих двух сил направлена вертикально вверх и представляет собой выталкивающую (архимедову) силу:

F_A=F₂ - F₁    (3)

Подставив (1) и (2) в (3), найдем, что модуль архимедовой силы

F_a=r_жg_lS=r_жgV = P_ж

где V - объем куба (т. е. объем жидкости, вытесненной погруженным телом); P_ж - вес вытесненной жидкости. Следовательно,выталкивающая сила по модулю равна весу жидкости, вытесненной погруженной частью тела.
Архимедова сила F_A приложена к телу в центре масс вытесненной телом жидкости и направлена против силы тяжести, действующей на это тело. (Необходимо помнить, что закон Архимеда справедлив только при наличии тяжести. В условиях невесомости он не выполняется.)

Условие плавания тел.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F_т и архимедовой силы F_A, которые действуют на это тело. Возможны следующие три случая:

F_т > F_A - тело тонет;

F_т = F_A - тело плавает в жидкости или газе;

F_т < F_A - тело всплывает до тех пор, пока не начнет плавать.