
Задачи олимпиад по физике 7 класс
Задачи олимпиад по физике 7 класс
Вар-т 3.
Трактор тянет широкозахватную сенокосилку со средней скоростью 6,28 км/ч. Какую площадь трав можно убрать за 8 часов работы, если тракторист обедал 30 минут, а ширина захвата сенокосилки 14,5 м?
Задача 2 :
В гонке участвуют 4 спортсмена, которые развивают разные скорости. Кто победит? Кто отстанет? Если первый спортсмен 165 м проходит 30 секунд, второй спортсмен 9,9 км за 30 мин., третий - 66 м за 2 мин., четвёртый 475.3 км за сутки.
Задача 3 :
У свинцовой пластинки определите толщину, её длина равна 40 см, ширина 2,5 см. Если пластинку опустить в стакан, до краёв наполненный водой, выльется 80 г воды.
Задача 4 :
Из двух сёл, расстояние между которыми 36 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 часа? На сколько км/ч пешеходы сближаются друг с другом (эту величину называют скорость сближения)?
Задача 5 :
Определите толщину одной страницы выданной книги.
Задача 6 :
Два спортсмена одновременно стартуют в противоположных направлениях из одной точки замкнутой беговой дорожки стадиона и к моменту встречи пробегают – один 160 м, а другой 240 м. При старте в одном направлении более быстрый спортсмен дает 100 м форы более медленному. Через сколько метров от точки старта он догонит соперника?
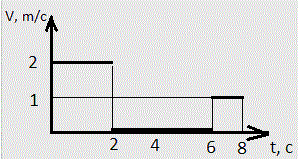
Задача 7 :
Зависимость скорости пешехода V от времени приведена на графике. Найти среднюю скорость пешехода за первые 8 секунд (4 балла). Найти среднюю скорость за большой промежуток времени, если, начиная с момента t = 6 с, скорость равна 1 м/c (6 баллов).
Задача 8 :
Два металла с плотностями 10500 кг/м3 и 19300 кг/м3 сплавляют, взяв в одном случае равные объемы этих металлов, а в другом – равные массы. Какой будет плотность сплава в первом (4 балла) и втором (6 баллов) случаях? Считать, что объем сплава равен сумме объемов сплавляемых металлов.
Задача 9 :
Самый быстрый круг был пройден в Италии в 1979 г. на автомобиле «Мерседес-Бенц»
за 1 мин 52,67 с при скорости 403,878 км/ч.
Какое расстояние было преодолено и какая работа совершена, если мощность двигателя 500 л. с. (1 л. с. = 735 Вт)?
Ответ: 5909 м; 41,3 МДж.
Задача 10 :
Экипаж самого тяжелого французского танка состоит из 13 человек.
Танк имеет 2 двигателя мощностью по 250 л. с. и развивает скорость до 12 км/ч.
Каково его тяговое усилие?
Ответ: 110,4 кН.
Задача 11 :
В треугольнике ABC две высоты ha и hb не меньше длин сторон, на которые они опущены.
Найдите углы треугольника.
Задача 12 :
Произвольный выпуклый четырехугольник разрезали на 4 части по прямым,
проходящим через середины его противоположных сторон.
Как из этих частей сложить параллелограмм?
Задача 13 :
Запись даты проведения олимпиады состоит из восьми цифр: 01.02.2005.
Найдите ближайшую будущую дату, в записи которой все цифры различ-ны.
Задача 14 :
Могут ли кубы двух последовательных натуральных чисел иметь одинако-вые суммы цифр?
Задача 15 :
На доске записано целое положительное число N.
Разрешается представить N в виде суммы двух натуральных слагаемых N = x + y, а затем заменить его числом M = x * y.
Можно ли с помощью таких операций получить из числа 5: а) число 2005; б) произвольное натуральное число?
Задача 16 :
Из картона вырезали два единичных квадрата, совместили их центры и склеили.
Какие значения может принимать отношение площади получен-ной фигуры к ее периметру?
Задача 17 :
На шахматной доске 8x8 разрешается перекрашивать в противоположный цвет сразу все клетки,
расположенные внутри квадрата размером 2x2.
Может ли при этом на доске остаться ровно одна черная клетка?
Задача 18 :
Если переписать в обратном порядке цифры некоторого пятизначного числа, то в результате получится число,
вчетверо больше первоначального.
Найдите это число.
Задача 19 :
Какое наименьшее число «уголков» из трех клеток нужно разместить в квадрате 8x8 клеток,
чтобы в него нельзя было больше поместить без наложения ни одной такой фигуры?
Вар-т 1 Вар-т 2 Вар-т 3 Задания с ответами