Олимпиады по физике 9 класс
Олимпиады по физике 9 класс с решением
Условие:
Определите коэффициент трения скольжения деревянной и пластмассовой линеек о поверхность стола.
Оборудование. Штатив с лапкой, отвес, деревянная линейка, пластмассовая линейка, стол.
Решение :
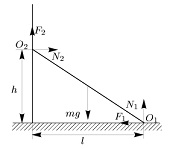
Рис. 2.
Закрепив в лапке штатива деревянную линейку, кладем на нее пластмассовую линейку. Изменяя угол наклона, добиваемся скольжения пластмассовой линейки по деревянной, тогда μ = tg α, где α – угол линейки с горизонтом. Закрепим деревянную линейку вертикально с помощью отвеса. Приставим к ней пластмассовую линейку и, изменяя ее угол β с горизонтом, добьемся скольжения ее скольжения по столу (рис. 2). В этом случае N2 = F1 = μ1N1, F2 = μN2. Моменты сил относительно точек O1 и O2 должны быть нулевыми:
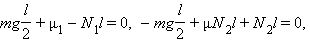откуда μ1 = l / (2h + μl). Аналогично определяется μ2.Задача 2 :
В закрытый вагон, стоящий на рельсах, проложенных по горизонтальной поверхности, сел человек, у которого имеются пружинные весы и секундомер. Сидя лицом по направлению движения вагона (вдоль рельсов) и прицепив к пружинным весам грузик массой т, человек стал наблюдать за направлением отклонения грузика и показаниями весов, фиксируя те моменты времени, когда показания изменялись.Вагон пришел в движение и первые t1 = 4 с грузик был отклонен к человеку, а весы показывали 1,25mg; затем время, равное t2 = 3 с, грузик висел вертикально, а весы показывали mg. После этого грузик отклонился влево (поперек вагона) и при этом в течение времени t3 = 25,12 с весы опять показывали 1,25mg. Наконец, еще на протяжении t4 = 4 с грузик был отклонен вперед при тех же показаниях весов.Определите, где относительно своего первоначального положения оказался вагон и с какой скоростью он к этому моменту двигался. Считать, что при изменении направления отклонения и показаний весов человек сразу гасит рукой возникающие колебания.
Задача 3 :
В течение скольких земных суток Луна совершает один оборот вокруг Земли, если она движется по круговой орбите радиуса 3.8*10^8 м. Известно, что радиус Земли равен 6400 км., ускорение свободного падения на Земле 10м/с^2.
Задача 4 :
Человек массы 70 кг. поднимается по верёвочной лестнице к висящему в воздухе аэростату массой 350 кг. Когда ноги человека оторвались от Земли, аэростат находился на высоте 12 м. На какой высоте окажется человек, когда он доберётся до аэростата.
Задача 5 :
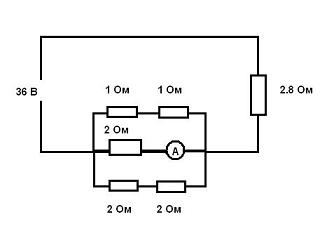
Найти силу тока в амперметре.
Задача 6 :
Для нагревания некоторой массы воды в электрочайнике от 22С до 100С потребовалось 5 минут. Удельная теплоёмкость воды равна 4.2 кДж/(кг*К). Удельная теплота парообразования 2.3 МДж. Через сколько минут после закипания вся вода в чайнике обратится в пар, если мощность подвода тепла к чайнику постоянна, а теплоёмкостью чайника и потерями тепла можно пренебречь?
Задача 7 :
На упругую плиту свободно падают два стальных шарика: 1-й с высоты h1 = 44 см, 2-й с высоты h2 = 11 см спустя т секунд после 1-го. Через некоторое время т скорости шариков совпадают по модулю и направлению.Определите время т и интервал времени, в течение которого скорости обоих шариков будут равными. Считать, что шарики между собой не соударяются.
Задача 8 :
Вблизи поверхности земли свободно падает тело массой m. В некоторый момент времени в него попадает (и застревает) горизонтально летящая тяжелая пуля массой М.Как изменится время падения тела на землю? Определите время падения t тела, если известно, что пуля попала в тело на половине пути, а время свободного падения тела с той же высоты равно t0. Считать, что масса пули много больше массы тела (М » m). Сопротивлением воздуха пренебречь.
Задача 9 :
1. Даны квадратные трёхчлены
f1(x) = х2+2a1x+b1,
f2(x) = х2+2a2x+b2,
f3(x) = х2+2a3x+b3
Известно, что
а1а2а3 = b1b2b3
Докажите, что хотя бы один из этих трёхчленов имеет два корня.
Задача 10 :
Семь лыжников с номерами 1,2,...,7 ушли со старта по очереди и прошли дистанцию —
каждый со своей постоянной скоростью.
Оказалось, что каждый лыжник ровно дважды участвовал в обгонах.
(В каждом обгоне участвуют ровно два лыжника — тот, кто обгоняет, и тот, кого обгоняют.)
По окончании забега должен быть составлен протокол, состоящий из номеров лыжников в порядке финиширования.
Докажите, что в забеге с описанными свойствами может получиться не более двух различных протоколов.
Задача 11 :
Можно ли при каком-то натуральном K разбить все натуральные числа от 1 до K на две группы и выписать числа в каждой группе подряд в некотором порядке так, чтобы получились два одинаковых числа?
Задача 12 :
В треугольнике ABC угол А равен 60o. Пусть ВВ1 и СС1 биссектрисы этого треугольника.
Докажите, что точка, симметричная вершине А относительно прямой B1C1 лежит на стороне ВС.
Вар-т 1 Вар-т 2 Вар-т 3 Задания с ответами